ÖZET
Mühendislik bilimlerinde oldugu kadar fen-, iktisadi-,
sosyal-bilimlerinde de pek çok problemin çözümünde FEM, BEM gibi sayısal
hesap yöntemlerinin kullanımı
bilgisayarlardaki hızlı gelismelere paralel olarak gelismekte
ve yayğınlasmaktadır. FEM gibi aktuel hesap yöntemleri gümümüzde
bir nevi multi
fonksiyonal problem çözüm araçları, pek çok teknik problemin çözümünü açıklığa
kavusturan general anahtar olarak görülmektedir.
Araci kullanan yine insan bilgisiolacaktir.
Prensip olarak;
komplex bir yapı bütünü (sistemi) çok sayıdaki basit kısmi
sistemlere, yapı elemanlarına indirgenerek, çok sayıdakı parçalara
bölünerek deklem sistemi ile tanımlanmasıdır. Ve bu denklem
sisteminin bilğisayar destekli çözümüne gidilmesidir. Günümüzde hazır
paket proğramları, pek çok örnek problem çözümlerı ve ekrandakı diyalog seklindeki uygulamaları
sayesinde bu yöntemlerin kullanımı kolaylastırılmıstır. Buna rağmen bu yöntemlerin efektiv kullanımı için de ilğili
bilim dalı ile mesleki bilğilerine ihtiyaç vardır. Ve çok sayıdaki
örnek çözümlerle kullanım alıskanlığı
peklestirilmelidir.
Günümüzün aktüel hesap,
problem çözüm araçlarının kullanımı mühendislerin bilhassa genç mühendis
adaylarının iş bulma şansı için belirleyici bir kriter
olmaktadır. Akademik, mesleki kariyer için de kulanım bir ön
şart haline gelmiştir. Günümüzde pek çok işyerinin ürün ve
hizmet araştırma ve geliştirme birimlerinde,
ARGE-Çalışmalarında FEM ve versiyonları ile
çalışılmaktadır (ANSYS, ABAQUS, I-DEAS, SIMPACK, MATLAB,
CADFEM, CATIA, ...) Bildirinin esas amacı; FEM ve BEM gibi çok yayğın
kullanılan sayısal yöntemlerinin mühendislik eğitimindeki,
mesleğindeki önemine bir iki aktuel simultan örneklerle dikkat çekmektir. Ilğili
örnekler interneten indirelen uyğulmalarla bu bildiriye ek olarak sunumda
gösterilmesi düsünülmektedir.
Anahtar kelimeler: FEM, BEM, neural-network,
matrix, differential deklem sistemleri, aktuel hesap yöntemleri, mühendilik eğitimi,
ANSYS, ABAQUS, I-DEAS, SIMPACK, MATLAB.
1. GIRIS
Direkt analitik yollardan hesaplanamayan ve, veya
çok güç hesaplanabilen kompleks teknik problemler FEM, BEM sayısal
yöntemleri ile kabul edilebilir sonucla çözülebilmektedirler.
FEM, Ingilizcesi; Finite Elemente Methode, Türkçesi; Sonlu Elemanlar Metodu ve
BEM (veya REM) (Ingilzcesi; Boundary
Element Methode, Türkçesi;
Sınır Elemanları Metodu.) FE hesap yöntemi bilhassa mekanik
problemlerin çözümünde bilgisayar destekli olarak yoğun kullanılmaktadır. Çok faktörlü ve degiskenli komplex
problemlerin çözümünde daha emin değerlere
ulasmak için neural-net gibi hesap yöntemleri gelistirilmektedir. Pek çok
mühendislik problemleri, konstruksiyon ve -imalat resimleri, üç boyutlu
geometrik sekiller, imalat işlevleri, kontrolleri, teknik-Analizler,
testler FEM, BEM kullanımı ile çözülebilmektedir, sanal olarak
ekranda gösterilmektedir, /1-13/. Ilğili
bilim dalının pek çok mühendislik islerinin bilğisayar tarafından
yerine getirilebilinmesi, halledilmaesi için bilimsel çalismalar yoğun
sürdürülmektedir. Fabrıkalarda bilgisayar
destekli, robotlasan ve
otomatiklesen üretim metodlariyla pek çok isçi isini kaybederken benzeri fenomen ileride
mühendisleride beklemektedir! Ileride mühendislerin aktuel mesleki bilğileri
yaninda yaratiçilik vasifları değer
kazanaçaktır. Ilğili meslek dalında söz sahibi olabilmek için
sürekli bir yenilenme sart olaçaktır. Örneğin CAD, CIM gibi sistemlerin kullanımında bazı
aksaklıklar tespit edilmektedir. Bu sistemlerin günümüzün aktuel çözüm
yöntemleri ile daha iyi bir inteğrasyonu üzerinde durulmaktadır. Bilği
deposundan, araç menüsünden gerekli çözüm elemanları otomatik aranılarak
konstruksiyon ve imalat için gerekli çizimlerin ve imalat, produksiyon
islevlerinin çok daha az islem hacmıyla daha seri, ekonomik ve kaliteli
gerçeklestirilmesi üzerinde projeler yürütülmektedir, /11-13/.
Günümüzde pek çok zaman alıçı ve
masraflı küçük, büyük laboratuar deneyleri, testleri, işlevleri
FEM-Simultan yöntemleri ile de gerçekleştirilmeğe
başlanılmıştır. Örneğin, Gemi
Mühendisliğinde bazi akıskanlar mekaniği ile ilğili havuz
deneyleri, konstruktion çizimleri, gemi imalat resimleri, mukavemet, stabilitet
hesaplari geliştirilen programlarla bilğisayar ekranında
görüntülenerek gerçekleştirilmektedir. Bazı hallerde elde edilen sonuçlar,
datalar örneğin havuz deneylerinden daha doğru ve yanılma
payı daha azdır. Bu yöntemler diğer mühendisdlik alanlarındada,
(makina, gemi, uçak, otomobil, tasisat, ağır çelik konstruksiyonları,
insaat,..) bilhassa otomobil sanayinde
geniş bir kullanım alanı bulmuştur. Sekil1, Sekil 2
Konstruktion ve imalat ve ucak ile ilgili örnekler görülmektedir. Pek çok deneyler, testler, analizler
(örneğin; güvenlik, aeordinamik, dizayn, ömür,
dayanıklılık, maliyet, rekabet, risk,
) geliştirilen
hazır paket proğramları ile bilğisayar ekranlarında
gerçeğine çok yakın bir şekilde simule edilebilmektedir, yani
sanal olarak yapılabilmektedirler, /13/. Crash-testleri, (çarpma testleri)
ile otomobil karöserinde olası
deformasyon, biçim değisiklikleri
etkensel faktörlere ve konstruksiyon parametrelerine göre ekranlarda
sanal olarak izlenebilmektedir. Aninda kritik yerler tespit edilip gerekli
kontruktiv müdahaleler denenerek optimal düzeltmeker gerçeklestirilmekterdir.
Bu gelişmelere paralel olarak FEM ve
versiyonları yurtdışındaki mühendislik bölümlerinde
bilhassa makine mühendisliğinde mecburi ve seçmeli ders olarak (temel- ve
mesleki dersler) verilmeğe başlanılmıştır. Pek
çok dersin içeriğinde de yer almaktadır. Derslerle ilğili pek
çok problemler FEM, BEM yöntemleri kullananılarak örnek olarak
çözülmektedir. Son yillarda mühendisliğin yeni baski bazi temel ve mesleki
ders kitaplarının içeriklerinde (konstruktion, mukavemet, satik,
dinamik, matematik,... sözü sayısal
FEM çözüm yömtemleri integre edilmistir, örnek çözümler CD ekinde sunulmaktadır.
Özel sektörde çalısan mühendisler için de seminerler, kurslar
düzenlenmektedır. Geçiçi olarak Almanyada çalıstığım
bir üniversitede orta ögretim öğretmenlerine bu yöntemler hafta sonu kursları
ile öğretilmeğe gayret
ediliyordu. Üniversiteye baslayacak liseli üniversite adaylarin gerekli alt
yapi bilğileri ile baslamaları amaçlanıyordu! Aktuel problem çözüm
yöntemleri mühendisler için yeni işalanlarin açılmasına vesile
olmaktadır. Örneğin son yıllarda
sirketlere FEM, BEM hesap yöntemleri kullanılarak danısmanlık hizmeti
veren sirket v e mühendislik büroların sayısı hayli artmaktadır.
Bu vesile ile Türkiyedeki mühendislik
fakültelerinde de, bilhassa makine mühendisliği bölümlerinde derslerde,
ders içeriklerinde FEM, BEM, Neural-Network ve versiyonlarının
kullanımı daha yoğun bir şekilde öğretilmesinde yarar
vardır. FEM ve simultan
yöntemlerinin pratik ve teorie bütünü içerisinde mecburi ders olarak verilmesinde yarar vardir. Mesleki derslerin içerikleridde
de yer almalıdır.
Türkiye üniversitelerinde akademik kariyer yapmak
isteyen öğretim elamanları için bu bilğiler, en azından
ANSYS, ABAQUS, I-DEAS, MATLAB, CADFEM; gibi paket proğramların kullanımı
avatajlar sağlamaktadır. Bu proğramlarla çok basit problemeleri
bile cıddi bilimsel arastırma projeleri gibi satabilirsiniz. Göze hoşgelen
renkli süslü diyağramlarla veya çoğu kisi tarafindan anlasılamayan,
bilhassa eskilerin pek takip edemediği matematiksel, denklem sistemleri
ile yayın hazırlamak ve SCI
derğilerinde yayınlamak daha kolay ve avantajlı olmaktadır. Rektörlüklerden de her SCI-yayını
için 1000 dolara yakın ödül de çabası!! (Sekilcilikle ve belescilikle
üniversitelerin ününü, kalitesini yükselteceklerini sananlar kendi kendilerini
kandırıyorlar. O bin dolarlarla aktuel çözüm yöntemlerinin, çok
kullanılan bir iki hazır paket proğramın kullanım lisansını
ve doğru dürüst internet bağlantılı hızlı çalısan
bilğisayarları üniversiteye, öğrençi ve öğretim elamanları
için kazandirabilirler..... )
2. FEM, BEM HESAP YÖNTEMLERI
Pek çok teknik problem, teknik olusum, değiskenlik ve çok boyutlu
geometrik sekiller matematik deklem
sistemleri ile, (matrix-, diferensiyal ve integral deklem sistemleri) tanımlanmaktadırlar.
Diğer taraftan Materyal bağıntıları, (Hooke gibi; s ~ e ) gibi matematik denklemlerin geçerliligi
basit elemanlar için geçerli olmaktadır, yani çözümü bulunmaktadır. Bu
denklemlerin pek azı analitik hesap yöntemleri ile direkt çözülebilmektedir.
Analitik yoldan çözülemeyen ve veya çözülmesi zor, karmasik olan
problemler numerik hesap yöntemleri kullanılarak
kabul edilebilir bir çözüme varılmaktadır. Bu yöntemlerden biri de FEM´dir, BEM´ dir.
BEM daha çok alansal, teknik yüzeylere ait problemlerin çözümünde FEM´ye
daha az sayıda islemlerle doğruluk
oranı yüksek, emin olusu nedeniyle terçih
edilmektedir. FEM genelde üç boyutlu problem bütününü yüksek dereceli denklem
sistemleri, diferensiyal denklem sistemlerini ele alırken BEM
alansal olarak problem bütününü inteğral denklemleri ile kurmaktadır.
REM´in 3 değisik uyğulama versiyonu vardır: a. Direkt
formulasyon veya direkt REM, ( intergral denklem sistemi, Elastizität problemi,
gerinme-gerilim), b. Yari indirekt formulasyon veya yarı indirek REM,
(intergral denklem sistemi, potansiyel problem, gerilim dağılımı),
c. indirekt formulasyon veya indirekte REM, ( Diferensiyal + Intergral denklem
sistemeleri). FEM denklemlerin kurulması
çok basit olmasına rağmen, çözüm için gerekli denklemlerin sayısı hayli fazladır. Çok basit
bir mukavemet, statik probleminin çözümünde bile denklem sayısı,
dolayıysla islem hacmi çok fazladır.
Bir Otomobil crash testinde kurulan
denklemlerin sayısı yüzbinlercedir. Yüklü bir container gemisinin fırtınalı denizdeki seyri sırasında
ortaya çıkan üç boyutlu zorlamaların
ve sekil değisikliğin tespiti
için kurulan denklemlerin sayısı milyonu bulmaktadır. Eskiden bu
boyuttaki problemlerin cözümünü Almanya, ABD, Japonya gibi ülkelerde sadece
büyük firmalar yüklü paralar ödeyerek ve bu alanda uzmanlasan sirketlere,
üniversitelere yaptırabılıyordu. Bu gün ise benzeri, hatta daha
kompleks problemler günümüzün 1000 ile 2000 dolarlık bilğisayarlarında
hazır paket proğramlar sayesinde çok çok daha kısa sürede rahatlıkla
gerçeklestirilebiliniyor.
Mekanik bilğilerini hatırlayanlar FEM,
sonlu elemenaler yöntemini çok daha iyi gözönünde bulundurabilirler ve rahatlıkla
kendi proğramlarını kurabilirler! Dişzorlamalara maruz
kalan teknik bir yapıda ortaya çıkan kuvet ve momentler, iç
gerilmeler ve olası geçiçi ve kalıcı sekil değisikliği,
deformasyon mekanik sistem ve veya serbest cisim diyağramı çizilerek
ve kontrolu istenilen yerin sanal kesimi düsünülerek rahatlıkla denğe
denklemleri kurularak çözülüyordu, Sekil
3. Sonlu elamanlar yöntemi de benzer sekilde düsünülebilir. FE-hesap
yönteminde teknik yapi bütünü çözüm
yöntemine uyğun çok sayıdakı parcalara, elemanlara, (Sekil 4) bölünmektedirler. Bu elamanlar birbirlerine
noktasal düğümlenmekte, yani bir nevı kontak noktları (düğüm
noktaları, irtibat noktaları, temas noktaları) ile bağlanmaktadırlar.
Bu düğüm noktaları vasıtasıyla kuvet ve momentler diğer
bir elemana aktarılmaktadır.
Sekil x. Gerinim-Gerilim hesap
yöntemine göre bu düğüm noktların
gerinimi, (yer değistirme, sekil değistirme mıktarı)
bilinmeyen olarak ele alınmaktadır. Materiyal bağıntıları,
(örneğin Hook-kanunu; s = E e ) dikkate alınarak düğüm noktalarında geçerli denğe
denklemleri yazılmaktadır. Elemanların seçimi teknik yapı
bütününe göre bir boyutlu, ( Cubuk, ), iki boyutlu alansal (levha, kabuk), üç
boyutlu, hacimsal olabilmektedir, Sekil x.
Elemanların sematik yapıları gösterilmektedir. Elemanlar
düz veya eğrisel olabilirler.
Elemanın seçimi, geometrik sekil ve boyutu, sıklığı
islem hacmını ve sonucun doğruluk oranını etkilemektedir.
Her geçen gün gelistirilen hazır paket proğramları, (ANSYS, I-DEAS, MATLAB...) ile FEM uyğulamaları
ekranda diyalog seklinde kolaylastırılmıstır. Örneğin
proğram menüsünden, Data-banktan elamanları tıklayarak teknik
yapınıza yerlestirebilir ve uyğun dağılımı
seçebilirsiniz. CADFEM bazlı hazir
paket proğramları ile Teknik yapi bütününü ekranda yansıtarak
FEM veya REM yöntemi ile teknik yapılarda gerilim dağılımı
ğibi hesap sonucları, analiz değerleri farklı diyağramalarla, tablolarla renkli gösterebilir,
bilinmeyen değerlerin hesabını gerçeklestirbilirsiniz, Sekil 6. Pek
çok değeri, teknik olanağı, teknik olusumu ekranda simultan
deneyebilirisiniz.
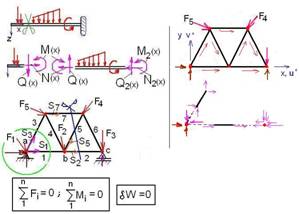
Sekil 3 Serbest çisim ve denge denklemleri

Sekil 4. Bazi eleman tipleri


Sekil 6.
V- ve I- kaynağında FE-ağ
örtüsü ve I kaynaginda gerilim dagilimi
Sekil 5 Bir
kranportalın yapısı dışzorlamalarla ve eleman ağı
ile görülmektedir. Kranportalın ayni kalınlıkta ve homogen bir
yapı malzemesine sahib olduğu varsayılmaktadır. FEM uyğulaması
için basit yapı sistemi 31 adet düz
ücgen tipi elemana bölünmektedir. Bu elamanlar kuvet ve momentleri, iç gerilmelerini
25 adet dügüm noktası ile aktarmaktadırlar. Eleman seçimi ve sıklığı
en küçük islem hacmıyla en doğru değere ulasabilecek sekilde
olmalıdır. Diğer alternativlerle denenmesinde ve kontrolunde
yarar vardır! Değisken yük,
q(x) ve diğer kuvet ve
momentlerin etkileri düğüm noktalarından
olmaktadır 1, 2, 3, 4, 5 mesnet düğüm nokataları hariç diğer
düğümler zorlamaların etkisi ile iki yönde gerinebilirler, yer değistirebilirler;
ve serbestlik dereceleri 2 dir. Bu
sayede 40 bilinmeyenli bir liner denklem sistemi ile çözülmektedir. Bu
denklemlerin matriks ile tanımlanması
rahatlık, hakimiyet sağlar.
Linear Denklem sistemi:
a11x1 + a12x2
+ ... + a1nxn = y1
a21x1 + a22x2
+... +a 2nxn = y2
: :
am1x1 + am2x2+ ... +amnxn =
ym
Matrix
denklemi, m x n Matriks:
|
a11 a12
... a1n |
|
x1 |
= |
y1 |
Ax = y : Vektoryel
A = aij : Bilinen katsayılar,
xn : Bilinmeyenler, sutün matrix vektörü,
(Tensör)
ym : Bilinen değerler, Satir matrix vektörü,
(Tensör)
Gerilim tensorü: S (hacimsal
eleman)
|
|
ax t xy txz |
|
s1 0
0 |
|
s = sx + sy + sz ; Toplam gerilim Gerinim,
sekil değistirme tensorü V, (hacımsal elaman) |
|
|
ex exy exz |
|
e1 0 0
|
s = E e ; Hooke kanunu
ex = ( du / dx) = 1/E (sx- v( sy + sz) ) + a DT
ayni sekilde ey, ez gerinmeleri icin bagintilar
......
.......
Deetaylı acıklamalar ve örnek çözümler bu
bıldırının kapsamı dışındadır. FEM
ve BEM ıle ılgılı cok sayıdakı lıteratür
bulunmaktadır.
3. FEM UYĞULAMA ÖRNEKLERI
Ilğili karekterisitik örnekler interneten indirelen uyğulamalarla bu
bildiriye ek olarak sunumda gösterileçektir. Lietratürde verilen
Web-sitelerinden, www.simtop.de karekteristik cok sayida uygulmalar aciklamalariyla verilmektedir., Internetten
herkez tarafindan indirebilinir.
4. SONUÇLAR
Kısaca FEM, BEM, Neural Network v.b. hesap
yöntemleri genelde pek çok problemin çözümünü açıklığa
kavusturan anahtardırlar, çözüm araçlarıdır. Her geçen gün bu
yöntemler bilğisayarlardaki hizli
gelismelere paralel olarak gelismektedirler.
Mühendislik, fen, sosyal. İkstisadi, tip bilimlerinde kullanım alanları
genislemektedirler, yoğunlasmaktadır. FEM kendi basına kullanım
alanı genişbir bilim alanı haline gelmistir.
Su sıralar yurtdısında izlediğim
kadarıyla: Son beşyılda bilimsel proje çalısmaları; genel
olarak bilğisayar destekli bilği toplama, bilği ayıklama,
bilği sınıflandırma, bilği depolama, süratli bilği
değerlendirme, bilği kullanma yönünde yoğunlasmaktadır. Hedef
daha kaliteli, güvenilir ve ekonomik mal ve hizmet ürünüyle işpıyasasında
var olmadır, rekabet edebilir sansını korumaktır, yükseltmekdır.
Bunun içinde gerekli paket proğramları günümüzün aktuel sayısal çözüm
yöntemleri, neural ağ hesab çözüm yöntemleri, araçları kullanılmaktadır,
gelistirilmektedir. Ve kısa sürede çok sayıda emin, güvenilir değerlere
bilğilere varmak içinde simultan yöntemlerle testler, deneyler, geometrik
sekiller, teknik çizimler gerçeklestirilmektedir,
farklı parameterler denenmektedir.
Bu gelismelere paralel olarak günümüzün aktuel problem çözüm yöntemlerinin,
araçlarının üniversitelerimizde yoğun bir sekilde öğretilmesinde yarar vardır.
Bunun yanısıra üniversitelerimizin meslek kurulusları ile işbirliğine
giderek endüstride çalısan, ilği
duyan mühendislere seminerlerle, hafta sonu uyğulamali kurslarla bu bilğilerin
kazandırılmasına, araçların kullanılmasına çalısılmalıdır.
Yayğın kullanılan ilğili paket porğramlarının
kullanımı uyğulamalarla peklestirilmelidir.
Bilğisayar destekli aktuel problem çözüm
yöntemlerin bilğisi, kullanımı bilhassa yeni mezun olaçak gençlerin
işbulma sansını artıraçaktır. Akademik ve mesleki
kariyer içinde aktuel problem çözüm yöntemlerin bilğisi, araçların
kullanımı sart olmaktadır.
Konuyla ilğili tartısılması gereken bazı
sorunlar mevcuttur örneğin su anda ilk akla gelenler:
- Günümüzün aktuel FEM gibi sayısal problem
çözüm
yöntemlerinde mühendislik
öğrençilerine nelerin öğretilmesi,
nelerin
bilinmesi gerekliliği,
- Ilğili hang araçların, hangi
paket
proğramlarının
terçih edilmesi,
- Bazıları ise bu bilğilere fazla gerekli olmadığı,
fazla abartıldığı görüsündeler.
Firma için
gerekli proğramların dısarıda
uzmanlasan büro
ve
sirketlere yaptırılması,
gerektiğinde destek
alınması
daha karlıdır diyenlerde bulunmaktadır
LİTERATÜR
1. Müller, Günther Groth, Clemens.:FEM für
praktiker, 1. Grundlagen, 2. Strruktur
dynamik 2002, Expert-Verlag
2. Grot, Peter.: FEM-Anwendungen,
Statik,
Dynamik- und Potenzialprobleme mit
professioneller Software lösen Stinger-
Verlag, 2001
3. Ahlert, Helmut.: FEM. Finite-Elemente-
Methode
im konstruktiven Ingenieurbau
Werner-Verlag , Düsseldorf 2002
4. Klein, Bernd.: FEM. Grundlagen und
Anwendungen.., Vieweg Tascdfhenbücher,
2003
5. Woyand, Herbert.: I- DEAS praktikum
CAE/FEM Vieweg-Taschenbücher, 1999
7. Fritscher T., Zammert w., U.: FEM.-
Praxis
mit
ANSYS Vieweg-Verlag, Studium und
Technik, 1993
8. Knothe K.; Wessels H.: Finite
Elemente,
eine Einführung für Ingenieure,
Springer
Verlag,
1997
9. Klaus-Jurgen Bathe.:
Finite-Elemente-
Methoden, Sringer Verlag, 1986
10. Lorenz P., poterasu V., Mihalache N.: Methode der
Finiten Elemente und der
Randelemente Vieweg-
Verlag, 1995
11. PTK 2001, Vorträge, X. Internationales
Produktionstechnisches Kolloquim
TU-
Berlin, D-Berlin, 2001
12. IWF, TU: Jahresberichte 2000, 2001,
Poduktions Produktionstechnisches
Zentrum
Berlin.
13. www.simtop.de / www.ansys.com
/
www.abaqus.com / www.cadfem.de
/
www.i-deas.com /